Functional Principal Component Analysis

Functional Principal Component Anlaysis (FPCA)란 이름 그대로 functional data에 적용하는 PCA 방법
일반적으로 잘 알려져 있는 multivariate PCA는 $p$개의 변수를 $q(\ll p)$개의 변수로 차원축소(dimension reduction)하는 방법으로 각 변수들이 uncorrelated되기 때문에 회귀분석(regression)에서 흔히 발생하는 다중공선성(multicolinearity)을 해결할 수 있는 대표적인 방법임

Functional data??

Functional data란 여러 개체가 각각 시간이나 위치 등에 따라 관측된 형태를 보이는 데이터로 보통 종단자료(longitudinal data) or 시계열(time series) 데이터를 다른 관점에서 본 경우입니다.
시간에 따라 관측된 데이터를 연속(continuous)인 곡선(curve) 형태로 보고 분석하는 데이터 형태입니다.
Smootheness를 가정하고 있기 때문에 smoothing 방법이 필요하게 됩니다.
B-spline, wavelet basis 등의 basis function을 사용하여 smoothing하게 되고 basis 개수에 따라 smoothing 정도가 결정됨
하지만 형태가 복잡해지는 경우, smooth basis function의 개수가 많아져 차원이 커지는 문제 발생 $\Rightarrow$ 차원축소 방법이 필요!!

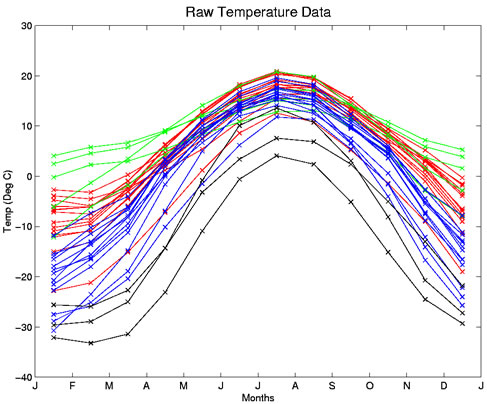
캐나다 35개 지점의 월별 기온 데이터(출처: Functional Data Analysis Website)

Functional PCA도 역시 dimension reduction 방법으로 basis fuction의 dimension을 줄여주는 방법
PCA와 마찬가지로 covariance matrix를 고유값 분해(eigenvalue decomposition)를 통해 구하게 됨
Smoothness를 가정하기 때문에 inner product가 새롭게 정의됨 \[ \langle x, y \rangle = \int x(t)y(t)dt \]

PCA와 마찬가지로 데이터의 평균(mean)을 빼어 centering한 후에 계산된 covariance matrix를 고유값 분해(eigenvalue decomposition)하여 구할 수 있음

Define the covariance function

\[ v(s,t) = \frac{1}{N}\sum_{i=1}^N x_i(s)x_i(t) \] where $x_i(t)$ is centerized.
Each of PC weight functions(or loadings) satisfies follow eigenequation

\[ \int v(s,t)\xi(t)dt = \rho \xi(s) \] or another form using covariance overator $V$,

\[ V\xi = \rho \xi \] where $ V= v(,t)(t)dt $ and $\xi$ is an eigenfunction.
Apply eigenvalue decomposition to above eigenequation
- The eigenfunction $\xi$ be the PC weight function.

구할 수 있는 eigen pairs의 개수가 다름
- Multivariate : # of eigen pairs = $p$ (raw data의 dimension)
- Functional : # of eigen pairs = $\infty$ ($\because$ smootheness)
Smoothness 가정
- 이 가정으로 인해 multivariate PCA에서 $\sum$으로 구하게 되는 inner product가 functional PCA에서는 $\int$로 구하게 됨